데이터 분석에서 고유값과 고유벡터의 중요성

고유값(Eigenvalue)과 고유벡터(Eigenvector)

정방행렬 $A$에 대해

\[A\mathbf{v}=\lambda\mathbf{v}\]

를 만족하는 $\mathbf{0}$이 아닌 열벡터 $\mathbf{v}$를 고유벡터, 상수 $\lambda$를 고유값이라고 한다.
$\lambda$를 ‘행렬 $A$의 고유값’, $\mathbf{v}$를 ‘행렬 $A$의 $\lambda$에 대한 고유벡터’라고 부른다.

행렬 $A$를 선형변환으로 보면, $A$에 의한 선형변환 결과가 자기 자신의 상수배가 되는 $\mathbf{0}$이 아닌 벡터가 고유벡터인 것이다.
기하학적으로 고유벡터는 선형변환 $A$에 의해 방향은 보존되고 scale만 변화되는 방향 벡터이며, 고유값은 그 고유벡터의 변화되는 scale의 정도를 나타내는 값이다.

고유값과 고유벡터는 행렬에 따라 정의되는 것으로, 행렬이 $n \times n$ 정방행렬인 경우 고유값과 고유벡터의 개수는 0개에서 최대 n개까지 존재할 수 있다.

공분산 행렬

각 feature의 분산으로 주 대각 원소들을 채우고, feature 간의 공분산으로 나머지 원소들을 채운 정방행렬이 공분산 행렬이다.

공분산 행렬을 선형변환으로 보면, 공분산 행렬의 고유벡터는 데이터의 분산이 커지는 방향을 의미한다.
그리고 각 고유벡터들의 고유값은 해당 방향으로의 분산의 크기를 의미한다.

주성분 분석(PCA)

주성분 분석은 데이터의 분산이 커지는 방향의 성분을 주성분으로 추출해 기존의 많은 feature들을 적은 수의 주성분으로 설명하는 기법이다.
따라서 공분산 행렬의 고유값과 고유벡터를 찾는 것은 데이터의 주성분을 찾는 것과 같다.

고유값이 클수록 해당 고유값에 대한 고유벡터 방향으로의 분산의 크기가 크다.
따라서 고유값이 큰 순서대로 해당 방향의 주성분들을 추출하고, 주성분의 개수를 적절히 선택해 차원을 축소할 수 있다.

이처럼 고유값과 고유벡터는 차원 축소에서 중요한 역할을 하며, 이외에도 데이터 변환, 변수 간 상관성 분석 등 다양한 분야에서 필수적인 도구로 사용된다.

(참고) 주성분의 개수를 선택하는 방법

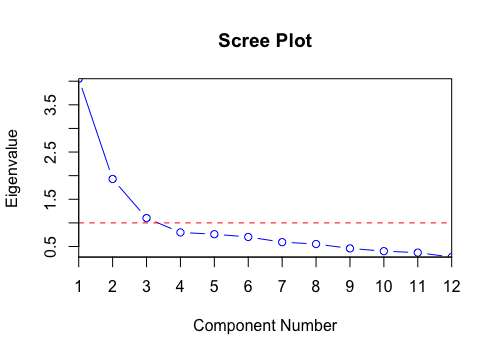
주성분의 개수는 Scree Plot을 그려 급격히 완만해지는 지점에서 끊어 직전까지의 개수로 정하거나, 누적 기여율을 계산해 85% 이상을 설명하는 최소의 개수로 정한다.